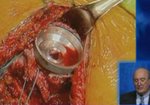
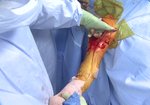
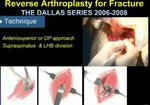
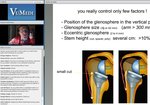
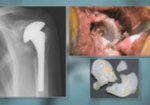
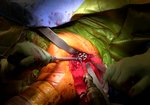
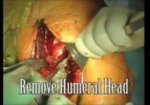
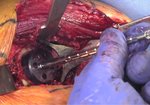
Preoperative shoulder planning; data matrix and visualization

By Michael Messieh 4 Videos FEATURING Michael Messieh

65 views

September 25, 2023

An educational research tool to stimulate discussion, Not intended for medical use;
On the AP ...
read more ↘ view, the fact that nodes C and G have significant contributions to both PC1 and PC2 suggests that they are nodes with strong influence on the overall variation in the dataset.
Node C is particularly interesting because it has a strong negative influence on PC1 and a positive influence on PC2, which means it has a unique combination of effects.
The clustering of nodes A, F, and B on PC1 suggests that they have similar effects on the variation captured by PC1.
The clustering of nodes C and G on PC2 suggests that they have somewhat similar effects on the variation captured by PC2. Explained Variance Ratios:

PC1 explains 89% of the total variance.
PC2 explains 6% of the total variance.
Node Contributions:

Node G has a relatively lower contribution to PC1 (0.3458) and PC2 (0.2952) compared to some other nodes.
Pairs of Nodes:

Node G is part of several pairs, but none of these pairs have the highest contribution to PC1 or PC2. For example, the pair ('C', 'F') contributes the most to PC1, and the pair ('D', 'A') contributes the most to PC2. data points associated with node G do not exhibit a significant spread or variation along PC1 and PC2, which is why there may not be a visible ellipse around node G. This suggests that node G is not a distinct cluster in this two-dimensional PCA representation; instead, it appears to be less influential in terms of explaining the variation captured by PC1 and PC2 compared to other nodes.
---

A dendrogram is a tree-like diagram used in hierarchical clustering to visualize the arrangement of data points (or objects) in a hierarchical manner. A dendrogram can help visualize a hierarchical relationship. The lines connecting nodes in a dendrogram are called "branches" or "linkages." These branches show how data points are grouped or clustered together based on their similarities. The height or length of a branch represents the degree of dissimilarity between clusters. Shorter branches indicate that the data points are more similar, while longer branches indicate greater dissimilarity.
------
In a K-means clustering result, nodes are assigned to clusters based on their proximity to cluster centers. If nodes C and G are in cluster 1, nodes A and F are in cluster 2, and nodes B, D, and E are in cluster 0, it means that, according to the clustering algorithm, these nodes are more similar to other nodes within the same cluster than to nodes in different clusters based on the features used for clustering (in this case, PC1 and PC2 scores).
↖ read less

Comments 0

Login

Login

Join VuMedi

Preoperative shoulder planning; data matrix and visualization

Identity Reverse Shoulder - 135 / Uniform Bearing Surgical Considera…

Recommended

Live Reverse Total Shoulder Arthroplasty using a Deltopectoral Appro…

Reverse Total Shoulder Arthroplasty: Steps to get it right

Reverse Shoulder Arthroplasty for the Treatment of Proximal Humeral …

Reverse Shoulder Arthroplasty for Acute Proximal Humerus Fracture

Avoiding Complications with Reverse Shoulder Arthroplasty: My Best T…

Latissimus Dorsi Transfer Combined with Bio-RSA

Reverse Shoulder Arthroplasty - Introduction and History

Tricortical Iliac Crest Bone Graft for Glenoid Component Loosening a…

RSA for Proximal Humerus Fractures: Indications and Tips for Maximiz…

How to Expose the Glenoid? A Technique with a Release on the Humeral…

Comprehensive® Vault Reconstruction System Featuring Dr. Dines

Revision Shoulder Arthroplasty – 5 Humeral Techniques to Remember

Reverse Total Shoulder Arthroplasty - Technical Notes and Results

Reverse Shoulder Arthroplasty for 4-Part Fracture

Preventing Infection - Must Do vs Voodoo

Stemless RSA with BIO-RSA and MR Navigation

Total Shoulder and Reverse Total Shoulder Technique and Nuisances

Prosthetic Replacement for Proximal Humeral Fractures - Current Conc…

Tornier Perform® Humeral System - RSA

MOSAIC 2024: Friday Morning